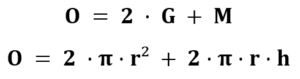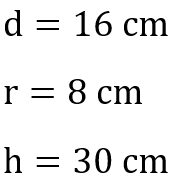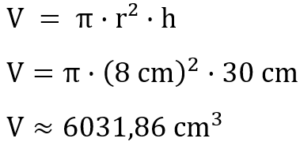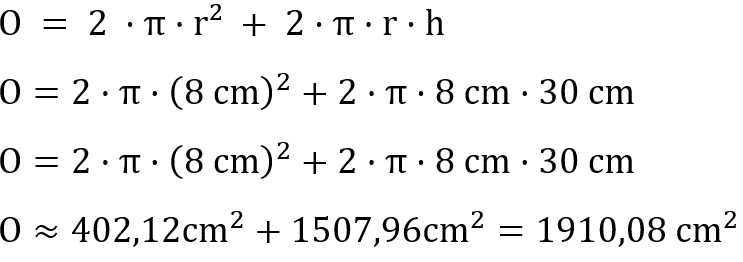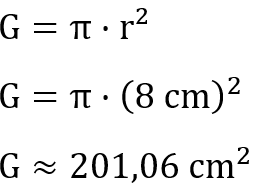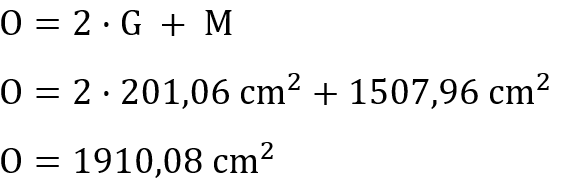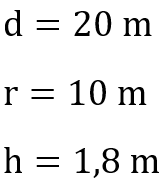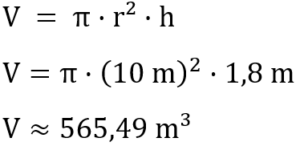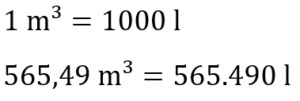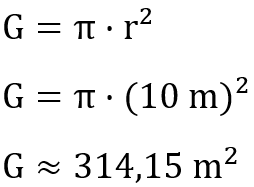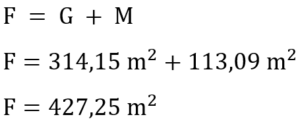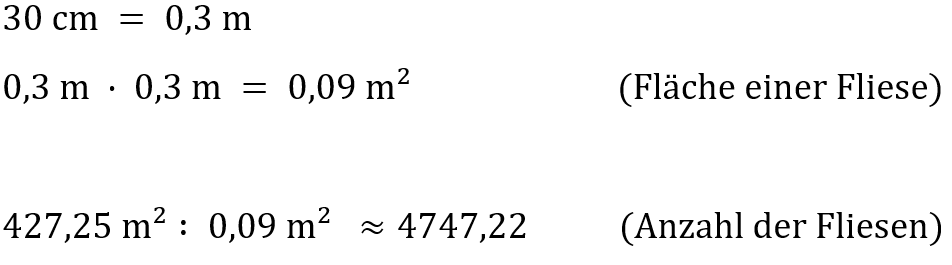Zylinder
Was ist ein Zylinder?
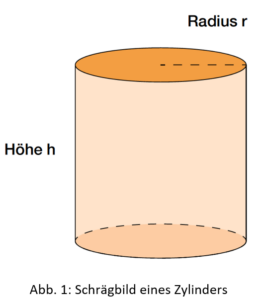
Ein Zylinder ist ein dreidimensionaler Körper, der als Grundfläche und Deckfläche einen Kreis hat. Die beiden Kreisflächen sind gleich groß und liegen dabei parallel zueinander. Die Seitenfläche ist ein (zusammengerolltes) Rechteck und wird als Mantelfläche bezeichnet.
Der Abstand der beiden Kreisflächen wird als Höhe h bezeichnet. Der Abstand vom Mittelpunkt eines Kreises bis zur Außenkante wird als Radius r bezeichnet.
Das Volumen des Zylinders
Das Volumen V eines Zylinders gibt an, wie viel in einen Zylinder hineinpasst. Man kann es sich so vorstellen:
Würdest du einen Zylinder mit Wasser füllen, so gibt das Volumen an, wie viel Wasser in den Zylinder hineinpasst.
Berechnet wird das Volumen des Zylinders mit der folgenden Formel.
Der Buchstabe G steht für die Grundfläche. Weil die Grundfläche ein Kreis ist, gilt Folgendes:
Das kann man in die Volumenformel einsetzen.
Beachte: In manchen Aufgaben findet man für die Höhe eines Zylinders die Angabe hK, was für die „Höhe des Körpers“ steht. Gemeint ist aber das gleiche Maß. Es kann aber auch sein, dass ein komplett anderer Buchstabe oder nur ein Maß für die Höhe des Zylinders angegeben wird.
Die Oberfläche des Zylinders
Stellt man sich vor, dass man einen Zylinder in der Hand hat, so besteht die Oberfläche O aus allen Flächen, die man von außen berühren kann. Man könnte auch sagen, dass es alle Flächen sind, die man von innen berühren kann. Man muss aber darauf achten, dass bei der Oberfläche immer nur eine Seite einer Fläche gezählt wird. Die Oberfläche des Zylinders berechnet man, indem man die einfache Fläche aller Teilflächen des Zylinders addiert.
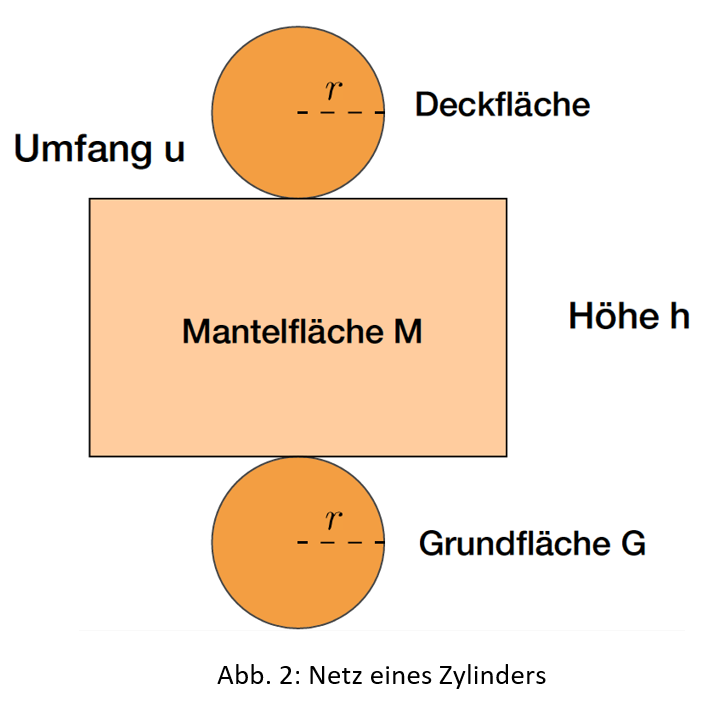
Um auf die Formel für die Oberfläche eines Zylinders zu kommen, hilft es, einen Zylinder auseinanderzufalten, sodass wir das Netz des Zylinders betrachten können.
Hier kann man erkennen, dass die Mantelfläche ein Rechteck ist und dass Grund- und Deckfläche zwei gleiche Kreise sind. Da Grund- und Deckfläche gleich sind und bei einem Zylinder auch gleich sein müssen, bezeichnet man sie beide mit dem Buchstaben G. Die Oberfläche des Zylinders ergibt sich, wenn alle Teilflächen zusammenzählt werden.
Wie bereits erwähnt, sind Grund- und Deckfläche gleich große Kreise, weswegen es ausreicht, die Grundfläche bzw. Deckfläche einmal auszurechnen und sie mit zwei zu multiplizieren.
Mantelfläche und Grundfläche des Zylinders
Die Grundfläche haben wir bereits im Abschnitt zum Volumen thematisiert. Für sie gilt nach wie vor die folgende Formel.
Bei der Mantelfläche müssen wir etwas genauer hinschauen. Die eine Seite unserer rechteckigen Mantelfläche ist die Höhe des Zylinders h. Die andere Seite ist der Umfang u unserer Kreisfläche. Setzt man das Netz wieder zu einem Zylinder zusammen, so muss man die Mantelfläche um die Kreisflächen rollen. Somit ist die eine Seite der Mantelfläche genauso lang wie der Kreisumfang. Für die Mantelfläche gilt also:
Die Formel für den Kreisumfang lautet folgendermaßen.
Eingesetzt in die Formel der Mantelfläche erhalten wir die folgende Formel.
Nun kann man die einzelnen Formeln für die Grundfläche und für die Mantelfläche einsetzen, um die Oberflächenformel direkt in Abhängigkeit vom Radius und von der Höhe zu erhalten.
Beachte: Auch wenn man einen liegenden Zylinder betrachtet, wird als Grundfläche immer die kreisförmige Fläche bezeichnet und als Mantelfläche immer die Seitenfläche.
Nun sind wir bestens vorbereitet, um einige Beispielaufgaben zu rechnen.
📌 Hat dein Kind noch Schwierigkeiten mit diesen Formeln?
Die Lernhilfe Sprenger bietet gezielte Nachhilfe in kleinen Gruppen oder als Einzelunterricht, um mathematische Konzepte spielerisch zu vermitteln!
Erfahre mehr über die individuellen Lernangebote.
Beispielaufgaben zum Zylinder
Beispielaufgabe 1: Eine Basisaufgabe zum Zylinder
„Ein Zylinder hat einen Durchmesser von 16 cm und ist 30 cm hoch. Berechne das Volumen und die Oberfläche des Zylinders.“
Lösung:
Wir notieren uns zunächst die benötigten Informationen aus der Aufgabe. Uns ist bekannt, dass wir für die Oberfläche und das Volumen den Radius r und die Höhe h benötigen. Hier müssen wir beachten, dass der Durchmesser d angegeben ist und wir daraus den Radius bestimmen können, welcher immer die Hälfte des Durchmessers ist.
Das Volumen
Für das Volumen gilt die im ersten Abschnitt angegebene Formel. Nun müssen wir nur die passenden Werte in diese Formel einsetzen.
Damit hat unser Zylinder ein Volumen von 108 cm³.
Beachte: Wenn wir Einheiten in unseren Rechnungen haben, so werden sie genauso wie Zahlen zusammengerechnet und anschließend wieder an das Ergebnis geschrieben. Beispiel: 1 cm · 1 cm = 1 cm²; 1 cm + 1 cm = 2 cm oder 2 m · 3 m · 4 m = 24 m³.
Die Oberfläche
Auch für die Oberfläche können wir nun die passenden Werte in die uns bekannte Formel einsetzen.
Der Zylinder hat also eine Oberfläche von 1910,08 cm².
In manchen Aufgaben ist zunächst nach der Grundfläche und der Mantelfläche eines Zylinders gefragt. Hier könnten wir auch schrittweise erst die Grundfläche und die Mantelfläche berechnen und diese nachher zur Oberfläche zusammenrechnen. Wir berechnen zuerst die Grundfläche des Zylinders.
Beachte: Wenn wir eine Länge anstelle von r² einsetzen, müssen wir beachten, dass wir den Wert in Klammern setzen. Ohne Klammer würde dort 8 cm² stehen und das hoch zwei würde sich lediglich auf die Einheit beziehen und das wäre falsch.
Nun benötigen wir noch die Mantelfläche. Wieder setzen wir die Werte in die richtige Formel ein.
Mithilfe dieser Werte kann nun die Oberfläche bestimmt werden, so wie es oben bereits erklärt wurde.
Hier kann man sich verdeutlichen, dass bei beiden Wegen der gleiche Wert für die Oberfläche herauskommen muss.
Für diesen Zylinder war die Rechnung noch recht simpel. Im Folgenden betrachten wir eine etwas komplexere Aufgabe, die an ein Beispiel aus dem Alltag angelehnt ist.
Beispielaufgabe 2: Eine Textaufgabe zum Zylinder
„Zur Eröffnung der Freibad-Saison wird Wasser in ein zylinderförmiges Schwimmbecken eingelassen. Das Becken ist insgesamt 1,80 m tief und hat einen Durchmesser von 20 m.
- a) Wie viel m³ Wasser passen in das Becken, wenn es bis obenhin gefüllt wird?
- b) Das Becken soll nach dieser Saison erneuert werden. Dazu sollen der Boden und die Wände des Schwimmbeckens mit 30 x 30 cm Fliesen neu ausgelegt werden. Wie viele dieser Fliesen werden benötigt?“
Lösung
Das Schwimmbecken in diesem Beispiel hat die Form eines Zylinders. In der Teilaufgabe a) ist gefragt, wie viel Wasser dort hineinpasst. Das bedeutet, es ist nach dem Volumen gefragt, welches wir nun berechnen. Auch hier notieren wir uns zunächst die für uns wichtigen Maße.
Wir setzen diese Werte in die Formel ein.
Da nach Litern (l) gefragt ist, müssen wir das Volumen in m³ in l umrechnen.
In das Schwimmbecken passen insgesamt also ca. 565.490 l.
In der Teilaufgabe b) ist nach der Anzahl der Fliesen gefragt, die zur Erneuerung des Schwimmbeckens verwendet werden soll. Hierzu müssen wir zunächst in Erfahrung bringen, wie groß die geflieste Fläche ist. Dass es nicht einfach nur die Oberfläche unseres Zylinders ist, werden wir gleich sehen.
Zunächst berechnen wir unsere Grundfläche, welche den Boden des Schwimmbeckens darstellt.
Als Nächstes müssen wir wissen, wie groß die Seitenflächen des Schwimmbeckens sind. Diese Seitenflächen sind die Mantelfläche des Zylinders.
Nun müssen wir die Grundfläche und die Mantelfläche zusammenrechnen, um auf die zu fliesende Gesamtfläche zu kommen. Man beachte hierbei, dass das Schwimmbecken sozusagen keinen „Deckel“ hat. Das heißt für die Fläche F, die gefliest werden soll, ergibt sich Folgendes.
Beachte: Hier wurde der Buchstabe „F“ für die Fläche gewählt, um deutlich zu machen, dass sich die Oberfläche in diesem Beispiel von der Oberfläche eines mathematischen Quaders unterscheidet, weil uns hier der „Deckel“ fehlt.
Im letzten Schritt muss nun bestimmt werden, wie viele Fliesen benötigt werden.
Für die Erneuerung des Schwimmbeckens werden also insgesamt 3840 Fliesen benötigt.
Wo findet man Zylinder im Alltag?
Im Alltag begegnen uns Zylinder wahrscheinlich häufiger als es zunächst erscheint. Am ehesten fällt uns der Hut eines Zauberers ein, der aufgrund seiner Form als Zylinder bezeichnet wird. Konservendosen sind typische Beispiele für Zylinder. Weitere typische Zylinder sind Küchenrollen, Gläser, Räder, Stangen, Eimer, Litfaßsäulen, Baumstämme, Batterien, Teelichter, Heuballen etc. Aber auch Münzen sind Zylinder, denn ein Zylinder muss nicht unbedingt eine bestimmte Höhe haben, sondern kann auch ganz flach sein. Man muss aber berücksichtigen, dass viele Körper nur annähernd Zylinder sind, da sie häufig an manchen Stellen etwas breiter oder etwas schmaler sind. Für das Berechnen von Volumen oder Oberfläche sind diese vereinfachten Annahmen aber mehr als hilfreich.
📌 Möchte dein Kind den Zylinder sicher verstehen?
Die Lernhilfe Sprenger bietet individuelle Online-Nachhilfe mit gezielten Übungen.
Jetzt eine kostenlose Probestunde buchen und Mathe spielend meistern!