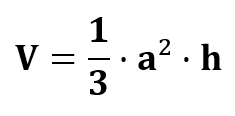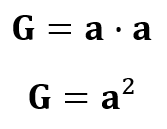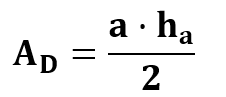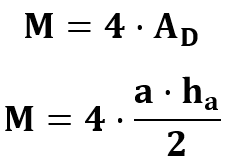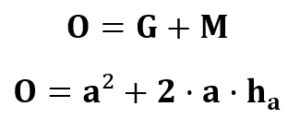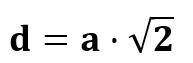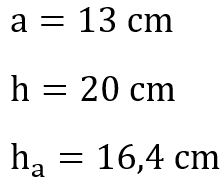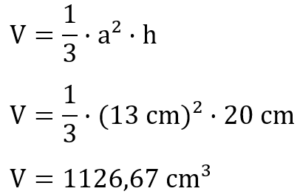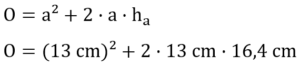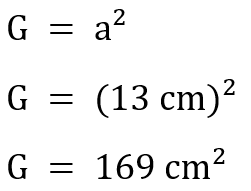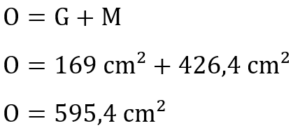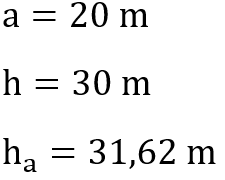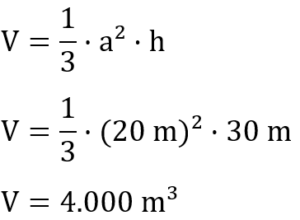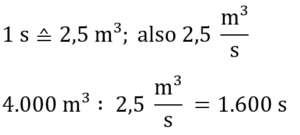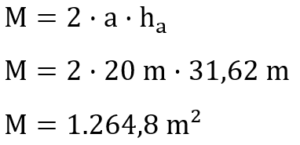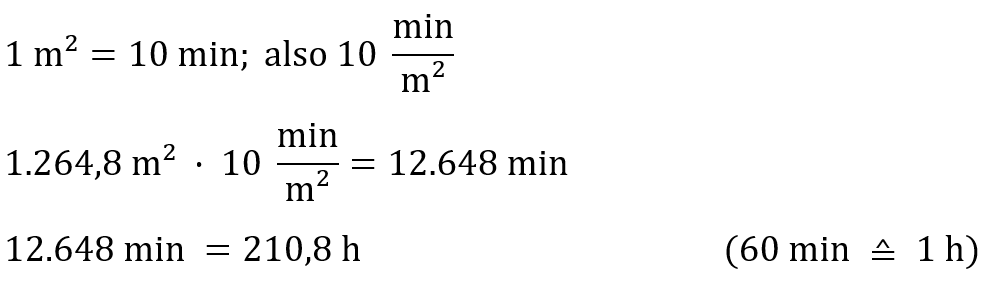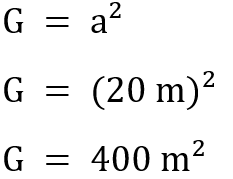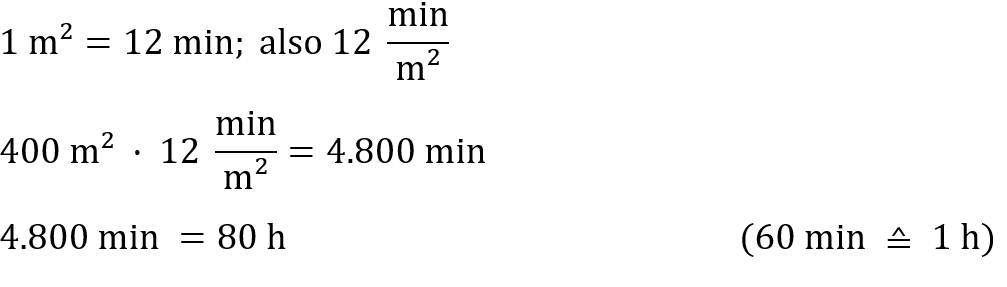Pyramide
Was ist eine Pyramide?
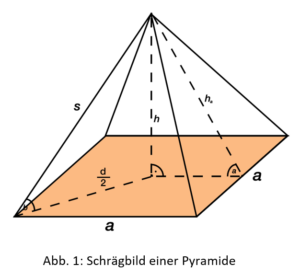
Eine Pyramide ist ein dreidimensionaler Körper mit einem Polygon (Vieleck) als Grundfläche. Die Seitenflächen der Pyramide sind Dreiecke, von denen jeweils eine Kante an der Grundfläche anliegt. Die jeweils gegenüberliegenden Dreiecksspitzen treffen sich alle in einem Punkt. Im Folgenden werden wir eine Pyramide mit einer quadratischen Grundfläche betrachten.
In der Regel bezeichnet man mit a die Kanten der Grundfläche. Die Höhe h der Pyramide ist der kürzeste Abstand von der Spitze bis zur Grundfläche und steht gerade dadurch senkrecht (also im 90° Winkel) auf ihr. Die Seitenhöhe ha ist in unserem Beispiel die Höhe über der Seite a und geht von ihr bis zur Spitze der Pyramide. Dann gibt es noch die Seitenkante s. Sie geht von einem Eckpunkt der Grundfläche bis zur Spitze der Pyramide. Die Diagonale d ist bei der Pyramide mit der quadratischen Grundfläche der Abstand zweier gegenüberliegender Eckpunkte der Grundfläche. Entsprechend ist d/2 der halbe Abstand zwischen den beiden Eckpunkten.
Beachte: Die verschiedenen Seitenlängen der Pyramide können auch mit anderen Buchstaben bezeichnet werden. Beispielsweise findet sich für ha auch die Variable hs, angelehnt an den Begriff „Seitenhöhe“.
Das Volumen der Pyramide
Das Volumen V einer Pyramide gibt an, wie viel in eine Pyramide hineinpasst. Man kann es sich so vorstellen:
Würdest du eine Pyramide umdrehen und mit Wasser füllen, so gibt das Volumen an, wie viel Wasser in die Pyramide hineinpasst.
Berechnet wird das Volumen der Pyramide mit der folgenden Formel.
Beachte: Wenn die Seitenlängen der Pyramide mit anderen Buchstaben bezeichnet werden, muss man die Formel an die Buchstaben anpassen.
Die Oberfläche der Pyramide
Stellt man sich vor, dass man eine Pyramide in der Hand hat, so besteht die Oberfläche O aus allen Flächen, die man von außen berühren kann. Man könnte auch sagen, dass es alle Flächen sind, die man von innen berühren kann. Man muss aber darauf achten, dass bei der Oberfläche immer nur eine Seite einer Fläche gezählt wird. Die Oberfläche der Pyramide berechnet man, indem man die einfache Fläche aller Seitenflächen addiert.
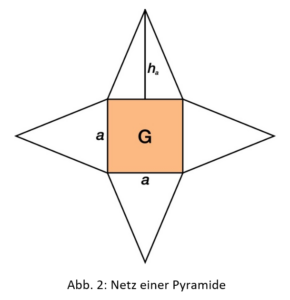
Um auf die Formel für die Oberfläche einer Pyramide zu kommen, hilft es, eine Pyramide auseinanderzufalten, sodass wir das Netz der Pyramide betrachten können.
Hier kann man erkennen, dass unsere Pyramidenoberfläche aus einem Quadrat, was unsere Grundfläche G darstellt, und aus vier kongruenten (deckungsgleichen) Dreiecken besteht, welche unsere Mantelfläche M bilden. Für die Oberfläche ergibt sich also die nachfolgende Formel.
Da die Grund- und Mantelfläche aus bereits bekannten Figuren besteht, können wir die Formel noch etwas weiter aufschlüsseln und die beiden Flächenabschnitte berechnen, was im nächsten Abschnitt demonstriert wird.
Mantelfläche und Grundfläche der Pyramide
Da die Grundfläche der Pyramide ein Quadrat ist, gilt diese Formel für die Flächenberechnung eines Quadrats.
Beachte: Die Grundfläche einer Pyramide kann neben einem Quadrat auch ein beliebiges Vieleck sein, z. B. ein Sechseck. Dann müsste man die passende Flächenformel für das Sechseck wählen, um die Grundfläche zu berechnen.
Die Mantelfläche besteht, wie wir gesehen haben, aus insgesamt vier kongruenten Dreiecken. Für die Fläche AD eines Dreiecks gilt die folgende Formel.
Da unsere Mantelfläche aus vier gleichen Dreiecken besteht, ergibt sie sich folgendermaßen.
Da die „2“ und die „4“ gegeneinander gekürzt werden können, kann die Formel noch weiter vereinfacht werden.
Nun kann man die Formeln für die Grundfläche und die Mantelfläche zusammensetzen, um auf die Oberflächenformel zu kommen.
Beachte: Auch wenn man eine liegende Pyramide betrachtet, wird als Grundfläche immer die Fläche bezeichnet, die nicht dreieckig ist und als Mantelfläche immer die Summe der Seitenflächen, die immer Dreiecke sind. Eine Ausnahme bildet hier die dreiseitige Pyramide, bei der die Grundfläche ebenfalls ein Dreieck ist und somit nicht mehr eindeutig von den Seitenflächen unterschieden werden kann.
Wie man bis hierhin sehen konnte, benötigten wir zur Berechnung von Volumen und Oberfläche das Maß für die Seitenkante s nicht. Es kann aber durchaus in mathematischen Aufgaben und in praktischen Zusammenhängen benötigt werden. Auf Basis des Satz des Pythagoras gelten die folgenden Formeln für s.
Die Diagonale kann ebenfalls mit dem Satz des Pythagoras bestimmt werden.
Nun ist es an der Zeit, das Wissen anzuwenden und einige Beispielaufgaben zum Thema zu rechnen.
📌 Hat dein Kind Schwierigkeiten mit diesen Formeln?
Die Lernhilfe Sprenger bietet gezielte Nachhilfe in kleinen Gruppen oder als Einzelunterricht, um mathematische Konzepte spielerisch zu vermitteln!
Erfahre mehr über die individuellen Lernangebote.
Beispielaufgabe zur Pyramide
Beispielaufgabe 1: Eine Basisaufgabe zur Pyramide
„Eine Pyramide mit quadratischer Grundfläche ist 13 cm hoch. Die Kantenlängen der Grundfläche sind 20 cm lang. Die Seitenhöhe ist 16,4 cm lang. Berechne das Volumen und die Oberfläche der Pyramide.“
Lösung
Wir notieren uns zunächst die benötigten Informationen aus der Aufgabe. Uns ist bekannt, dass wir für die Oberfläche und das Volumen die Kantenlängen der Grundseite a, die Höhe h und auch die Seitenhöhe ha benötigen.
Das Volumen
Für das Volumen gilt die im ersten Abschnitt angegebene Formel. Nun müssen wir nur die passenden Werte in die Formel einsetzen und berechnen.
Die Pyramide hat also ein Volumen von 1126,67 cm³.
Beachte: Wenn wir eine Länge anstelle von a² einsetzen, müssen wir beachten, dass wir den Wert in Klammern setzen. Ohne Klammern würde dort 13 cm² stehen und das hoch zwei würde sich lediglich auf die Einheit beziehen und das wäre falsch.
Die Oberfläche
Auch für die Oberfläche können wir nun die passenden Werte in die uns bekannte Formel einsetzen.
Die Pyramide hat also eine Oberfläche von insgesamt 595,4 cm².
In manchen Aufgaben ist zunächst nach der Grundfläche und der Mantelfläche einer Pyramide gefragt. Hier könnten wir auch schrittweise erst die Grundfläche und dann die Mantelfläche berechnen und diese nachher zur Oberfläche zusammenrechnen. Wir berechnen zuerst die Grundfläche der Pyramide.
Nun benötigen wir noch die Mantelfläche. Wieder setzen wir die Werte in die richtige Formel ein.
Mithilfe dieser Werte kann nun die Oberfläche bestimmt werden, so wie es oben bereits erklärt wurde.
Hier kann man sich verdeutlichen, dass bei beiden Wegen der gleiche Wert für die Oberfläche herauskommen muss.
Für diese Pyramide war die Rechnung noch recht simpel. Im Folgenden betrachten wir eine etwas komplexere Aufgabe, die an ein Beispiel aus dem Alltag angelehnt ist.
Beispielaufgabe 2: Eine Textaufgabe zur Pyramide
„Bei einem pyramidenförmigen Gebäude sollen die Innenwände, der Boden und die Lüftungsanlage erneuert werden. Das Gebäude hat eine quadratische Grundfläche und ist 30 m hoch. Die Breite des Gebäudes ist 20 m. Vom unteren Ende einer Seitenwand bis zur Spitze des Gebäudes sind es 31,62 m. Es sind immer die Innenmaße des Gebäudes gemeint.
- a) Wie lange dauert es in etwa, bis die ganze Luft im Gebäude einmal ausgetauscht wurde, wenn die neuen Lüftungsanlagen 2,5 m³ Luft pro Sekunde austauschen?
- b) Wie lange dauert die Erneuerung der Innenwände (in Stunden), wenn die Handwerker pro m² ca. 10 min benötigen?
- c) Wie lange dauert die Verlegung eines neuen Bodens, wenn für jeden m² 12 min benötigt werden?“
Lösung
In der Teilaufgabe a) ist gefragt, wie lange der Luftaustausch dauert. Hierzu müssen wir wissen, wie viel Luft in das Gebäude hineinpasst, es ist also nach dem Volumen gefragt. Auch hier notieren wir uns zunächst die relevanten Maße aus der Aufgabe.
Wir setzen die benötigten Werte in die Formel ein.
In das pyramidenförmige Gebäude passen also 4.000 m³ Luft. Jetzt muss noch berechnet werden, wie lange ein kompletter Luftaustausch mit der neuen Lüftungsanlage dauert.
Ein kompletter Luftaustausch würde also 1600 s dauern.
In der Teilaufgabe b) ist nach der Dauer zur Erneuerung der Innenwände gefragt. Angegeben ist, dass pro m² 10 min Zeit notwendig sind. Hier muss zunächst die Fläche berechnet werden. In diesem Fall handelt es sich um die Mantelfläche der Pyramide.
Nun muss noch berechnet werden, wie lange die Erneuerung der Fläche insgesamt dauert.
Die Erneuerung der Außenwände dauert 210,8 h.
In Aufgabenteil c) ist nun nach der Dauer für die Erneuerung des Bodens gefragt. Angegeben ist, dass pro m² 12 min Zeit notwendig sind. Auch hier ist wieder die Größe der Fläche notwendig. Hierbei handelt es sich um die quadratische Grundfläche unserer Pyramide.
Nun muss noch berechnet werden, wie lange die Erneuerung der Fläche insgesamt dauert.
Die Erneuerung des Bodens dauert also 80 h.
Wo findet man Pyramiden im Alltag?
Im Alltag begegnen uns Pyramiden nicht ganz so häufig wie Quader oder Zylinder. Am ehesten verbinden wir mit Pyramiden die großen Bauwerke der Ägypter, die Pyramiden von Gizeh, die auch als Grabkammern für Pharaonen dienten. Die womöglich Bekannteste und Älteste von ihnen ist die Cheops-Pyramide. Natürlich gibt es aber auch Souvenirs oder Süßigkeiten in Form von Pyramiden. Dort ist es im Rahmen der Produktion hilfreich zu wissen, wie viel Material zur Herstellung und Verpackung benötigt wird. Auch einige Dächer von Häusern oder auch von Kirchen sind pyramidenförmig. Dort ist es ebenfalls beispielsweise sehr hilfreich zu wissen, wie viele Dachziegel für das Decken des Daches benötigt werden.
📌 Möchte dein Kind die Pyramide sicher verstehen?
Die Lernhilfe Sprenger bietet individuelle Online-Nachhilfe mit gezielten Übungen.
Jetzt eine kostenlose Probestunde buchen und Mathe spielend meistern!