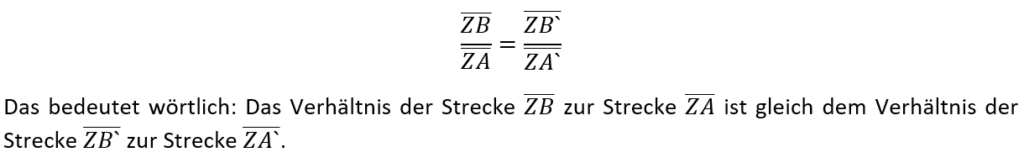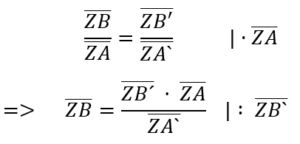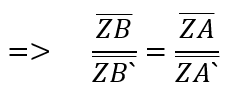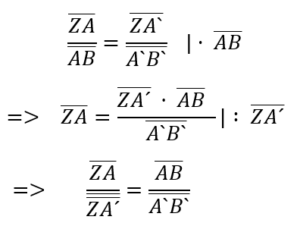Strahlensatz: 1. und 2. Strahlensatz
Der 1. Strahlensatz
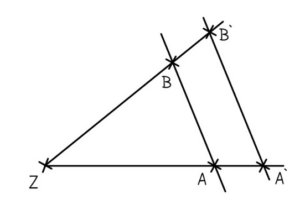
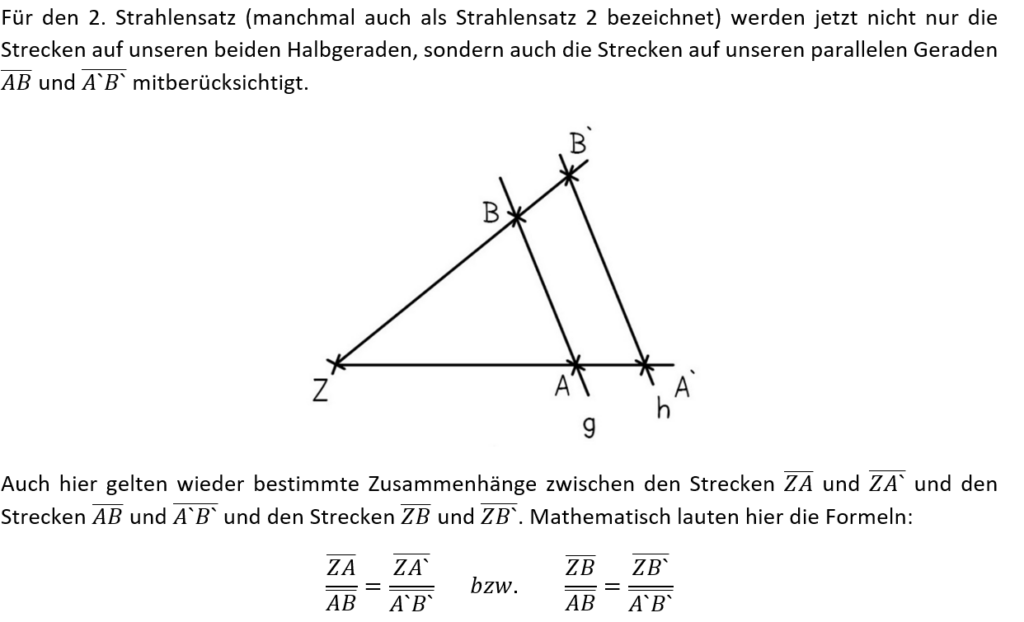
Im Mathe-Unterricht können mithilfe der Strahlensätze die Streckenlängen in bestimmten Aufgaben berechnet werden. Unsere zugrunde liegende Figur ist die folgende.
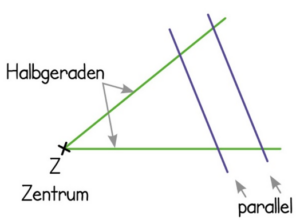
Wie zu erkennen ist, besteht sie aus zwei Halbgeraden gleichen Ursprungs und zwei parallelen Linien, welche die beiden Halbgeraden schneiden. Geben wir nun den einzelnen Schnittpunkten Bezeichnungen.
In dieser Figur gilt nun der sogenannte 1. Strahlensatz (manchmal auch als Strahlensatz 1 bezeichnet). Dieser sagt uns etwas über die Verhältnisse der einzelnen Teilstrecken aus. Es gilt die folgende Formel:
Mit dem 1. Strahlensatz kann nun immer die fehlende Strecke eindeutig bestimmt werden, wenn drei der vier Strecken gegeben sind. Diesen 1. Strahlensatz kann man auf viele Arten umstellen und ihn somit umformulieren. Es folgt eine beispielhafte Umstellung.
Mithilfe dieser Informationen kann man nun die Länge von einzelnen Teilstrecken berechnen.
📌 Hat dein Kind Schwierigkeiten mit dem Strahlensatz?
Die Lernhilfe Sprenger bietet gezielte Nachhilfe in kleinen Gruppen oder als Einzelunterricht, um mathematische Konzepte anschaulich zu vermitteln!
Erfahre mehr über die individuellen Lernangebote.
Der 2. Strahlensatz
Auch diese Formeln können nach Belieben umgestellt werden. Hier wieder eine beispielhafte Umstellung.
Es existieren viele Webseiten mit Übungen und auch Rechnern zur Bestimmung von Strecken in Strahlensatzfiguren, die du zur Überprüfung deiner Aufgaben verwenden kannst. Wir schauen uns nun aber an, wie man mit den Strahlensätzen auch ohne einen speziellen Rechner eine Aufgabe lösen kann.
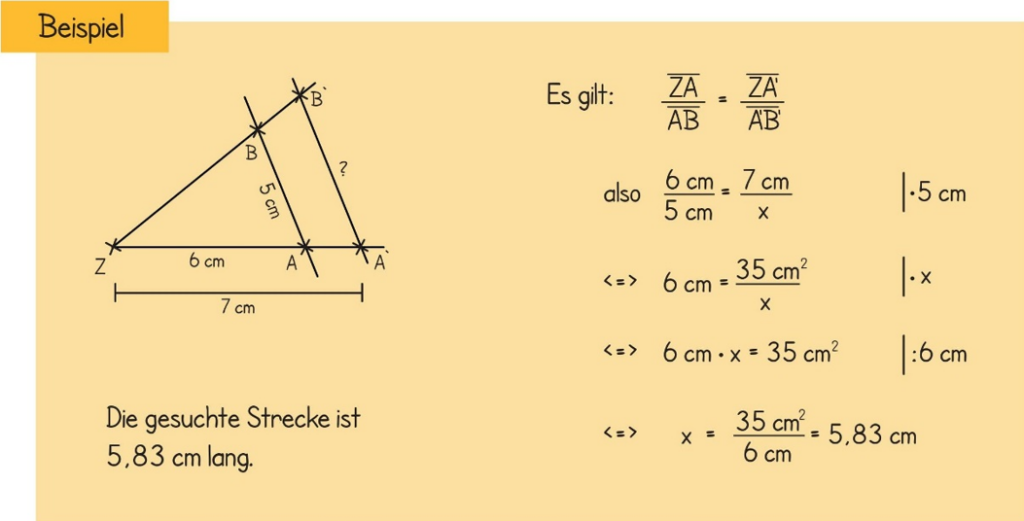
Eine unbekannte Strecke mithilfe des 2. Strahlensatzes berechnen
Wir betrachten nun, wie der 2. Strahlensatz zum Berechnen einer unbekannten Strecke verwendet werden kann.
Weitere Übungen und Aufgaben mit Lösungen als PDF findest du auf unserer Webseite.
Vermischte Aufgaben – Textaufgaben 1. Strahlensatz
1. Aufgabe 1. Strahlensatz – Lernschwierigkeitsgrad mittel
Klaus ist begeisterter Schwimmer. Da er nun an einem Wettbewerb teilnehmen möchte, hat er sich einen See in der Nähe gesucht, in welchem er gut trainieren kann. Leider konnte ihm die Mitarbeiterin nicht sagen, wie breit der See ist. Er weiß nur, dass vom Seeufer, also dem Zentrum (B), es 240 Meter bis zu seinem Liegeplatz (I) sind. 560 Meter in die andere Richtung (J) haben es sich ein paar Freunde gemütlich gemacht. Wenn man von ihrem Liegeplatz eine Diagonale zieht, erreicht man exakt das andere Ufer (A) des Sees. Wenn man vom Seeufer gerade weggeht, befindet sich in 160 Metern Entfernung (K) die Kantine. Es stellt sich nun die Frage, wie breit der See ist. Berechne die Entfernung der Punkte A und B.
Lösung:
I ZA I = x
I ZA‘ I = 160 Meter
I ZB I = 560 Meter
I ZB‘ I = 240 Meter
1. Aufgabe 1. Strahlensatz – Lernschwierigkeitsgrad mittel
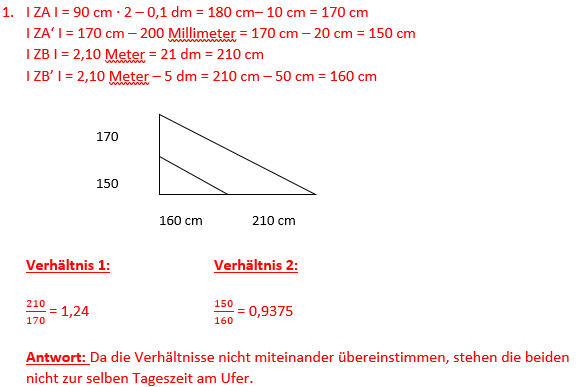
Martin und Jutta gehen gerne spazieren. Heute haben sie sich für einen Spaziergang am Fluss entschieden. Nun stehen die beiden am Flussufer. Jutta ist ungefähr 200 Millimeter kleiner als Martin. Martin ist doppelt so groß wie ihr Sohn Ludwig, wobei davon noch 0,1 dm abgezogen werden müssen. Ludwig hat eine Größe von 90 cm. Der Schatten von Martin ist 2,10 Meter lang. Während der Schatten von Jutta um 5 dm kleiner ist. Das Zentrum bilden die Füße der beiden (Z). Stehen die beiden zur selben Zeit am Ufer?
Lösung:
Vermischte Aufgaben – Textaufgaben 2. Strahlensatz
1. Aufgabe 2. Strahlensatz – Lernschwierigkeitsgrad mittel
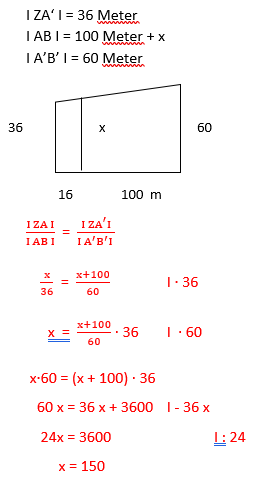
Klara hat sich ein neues Grundstück gekauft. Sie möchte sich gerne ein Haus darauf errichten lassen. Der Grundschnitt des Grundstückes hat die Form eines Trapezes. Die Seite a dieses Trapezes hat eine Länge von 100 Meter. Die Seite b entspricht einer Länge von 60% der Seite c und die Seite c Länge von 60 Metern. Als sie gerade dabei ist, mit der Planung des Hauses zu beginnen, stellt sich heraus, dass ihr Grundstück doch nicht so groß ist, wie ursprünglich angenommen. Der Nachbar hat sich beschwert, dass die Seite a des Grundstücks um 160 dm zu lang ist. Damit würde sich aber auch die Höhe der Seite b verändern. Nun fragt sich Klara wie lang die Seite b ist. Berechne die Länge der Seite b.
Lösung:
a = 100 Meter
b = 60% von 60 Meter = 60% ∙ 60 Meter = 36 Meter
c = 60 Meter
I ZA I = x
📌 Möchtest du, dass dein Kind die Strahlensätze sicher versteht und problemlos anwendet?
Die Lernhilfe Sprenger bietet individuelle Online-Nachhilfe mit gezielten Übungen.
Sichere dir eine kostenlose Probestunde und erleichtere deinem Kind das Lernen!