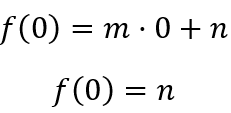Lineare Funktionen
Allgemeine Definition und Erklärung einer Funktion
Eine Funktion ist eine Zuordnung, bei der einem Wert aus einer sogenannten Definitionsmenge genau ein Wert aus einer sogenannten Wertemenge zugeordnet wird. Eine alternative Erklärung ist: Es wird einem x-Wert (aus der Definitionsmenge) genau ein y-Wert (aus der Wertemenge) zugeordnet. Die Zuordnung erfolgt mithilfe einer sogenannten Funktionsvorschrift. In der Mathematik findet diese Zuordnung in der Regeln in Form von Zahlen statt. Das bedeutet einer Zahl x wird genau eine Zahl y zugeordnet. Die Zuordnung erfolgt mithilfe einer sogenannten Funktionsvorschrift.
Für f(x) kann nun eine Funktionsvorschrift vorgegeben sein. Diese sagt uns, wie man mithilfe eines Wertes für x, den zugehörigen Wert für y berechnen kann.
Funktionswerte berechnen und einen Funktionsgraphen zeichnen
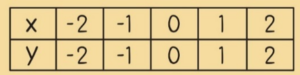
Wir wollen im Folgenden beispielhaft eine Aufgabe lösen, bei der man einen Funktionsgraphen mithilfe einer gegebenen Funktion zeichnen soll. Hier ist eine der einfachsten Funktionsvorschriften gegeben, um von einem Wert x zu einem Wert y zu gelangen.
Wenn wir für x nun verschiedene Zahlenwerte einsetzen, können wir die zugehörigen Zahlenwerte für y berechnen, was sich hier recht simpel gestaltet.
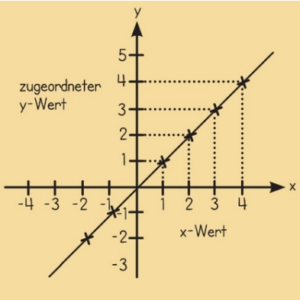
Diese Zahlenwerte kann man in ein Koordinatensystem zeichnen, um den zugehörigen Funktionsgraphen zu erhalten. Dieser entsteht durch die eingezeichneten Punkte. In diesem Fall ist unser Funktionsgraph eine Gerade.
Da der y-Wert direkt abhängig von dem x-Wert ist und sich aus diesem ergibt, nennt man den y-Wert auch den Funktionswert von x, welcher auch als f(x) bezeichnet wird. Somit kann man unsere Beispielfunktion auch schreiben als:
Lineare Funktionen
Für die Zuordnungsvorschriften einer Funktion gibt es zahlreiche Möglichkeiten. Wir betrachten nun die sogenannten linearen Funktionen. Diese Klasse von Funktionen sieht bspw. wie folgt aus.
Die Zuordnungsvorschrift für diese Funktionen hat immer die Formel:
Unsere Variable x wird mit einer Zahl m multipliziert und anschließend mit einer Zahl n addiert. Hierbei ist m die Steigung unserer Funktion und n der y-Achsenabschnitt. Was es genau damit auf sich hat, werden wir gleich anhand der grafischen Darstellungen verdeutlichen.
Der y-Achsenabschnitt n einer linearen Funktion
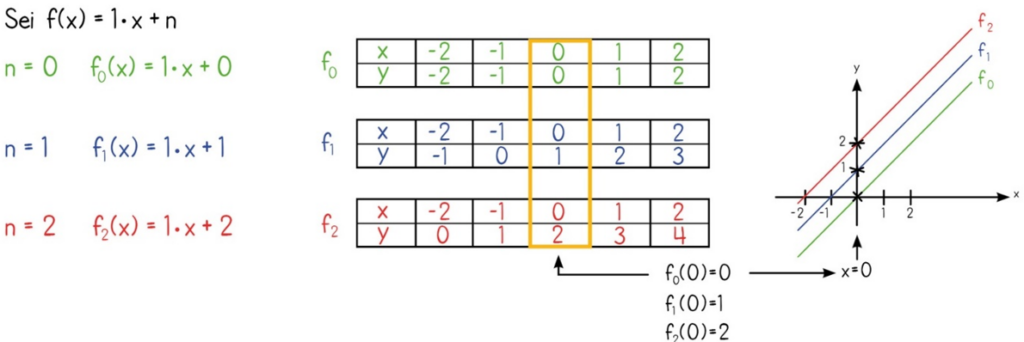
Wir betrachten nun eine Reihe von Funktionen (f0, f1, f2), für die m = 1 gilt und n variiert wird.
Es ist erkennbar, dass der Funktionswert an der Stelle x = 0 dem Wert von n entspricht. Da an der Stelle x = 0 auch die y-Achse verläuft, ist es auch gleichzeitig der Wert, an dem die Graphen die y-Achse schneiden. Hierbei handelt es sich um den y-Achsenabschnitt.
Anhand der Funktionsvorschrift erkennt man: Wenn für x der Wert 0 eingesetzt wird, ist das Produkt aus m und x gleich 0. Es folgt, dass n nun den Funktionswert angibt.
Der Funktionswert an der Stelle x = 0 ist für lineare Funktionen also immer gleich n.
Die Steigung m einer linearen Funktion
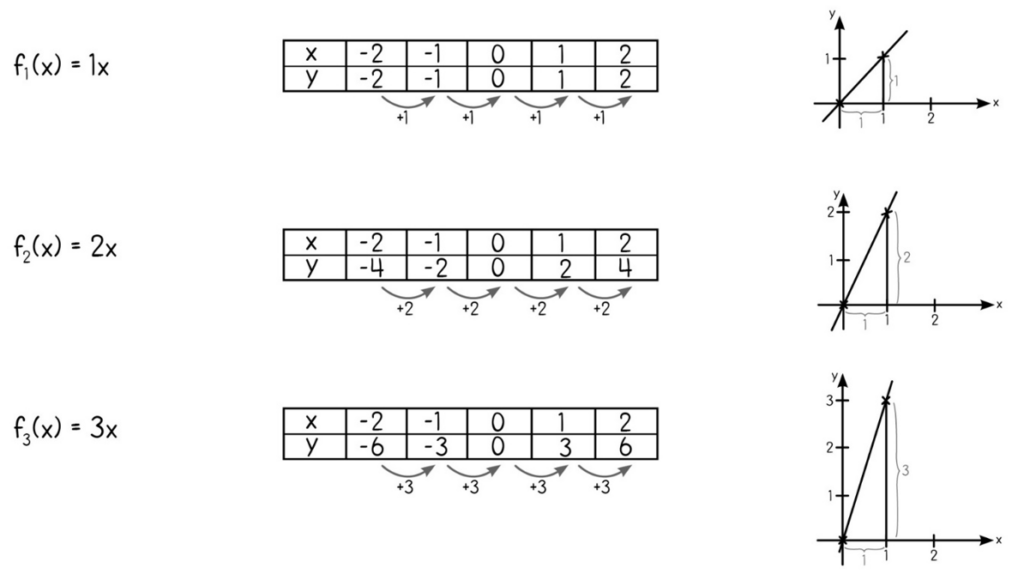
Wir betrachten nun eine Reihe von Funktionen (f1, f2, f3) für die n = 0 gilt und m variiert wird.
Es ist erkennbar, dass mit steigendem Wert für m der Funktionsgraph steiler ansteigt. Der Wert für m gibt mir also an, um wie viel mein y-Wert größer wird, wenn ich meinen x-Wert um 1 erhöhe.
📌 Hat dein Kind Schwierigkeiten mit diesen Formeln?
Die Lernhilfe Sprenger bietet gezielte Nachhilfe, um Mathematik verständlich und spielerisch zu erklären! Erfahre mehr über die individuellen Lernangebote.
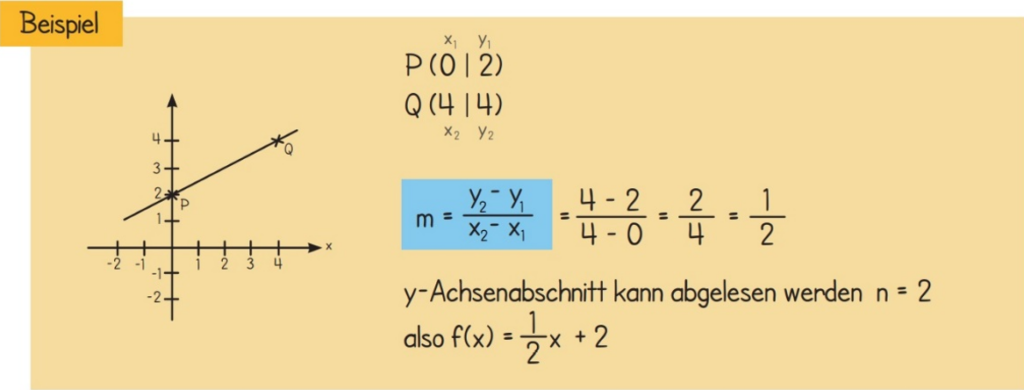
Eine Beispielaufgabe zur Berechnung der Steigung
In vielen Aufgaben ist die Steigung nicht angegeben. Jedoch kann man sie mithilfe von zwei Punkten, die auf dem zugehörigen Funktionsgraphen liegen, berechnen. Es gilt:
Zur Erklärung dient das folgende Beispiel.
Aufgaben zum Thema lineare Funktionen
Graphen zeichnen
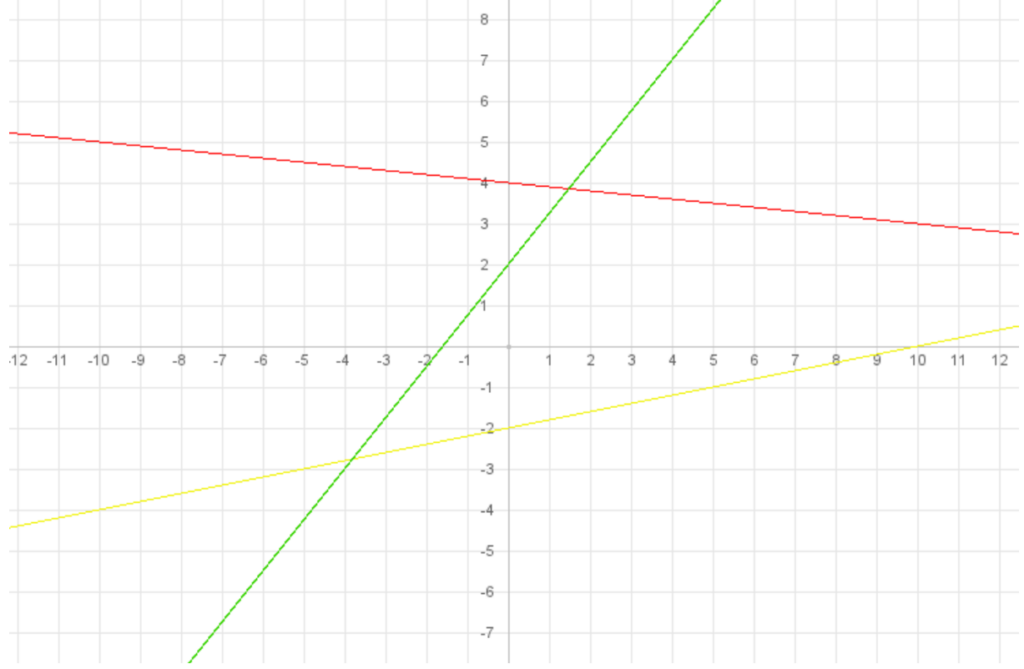
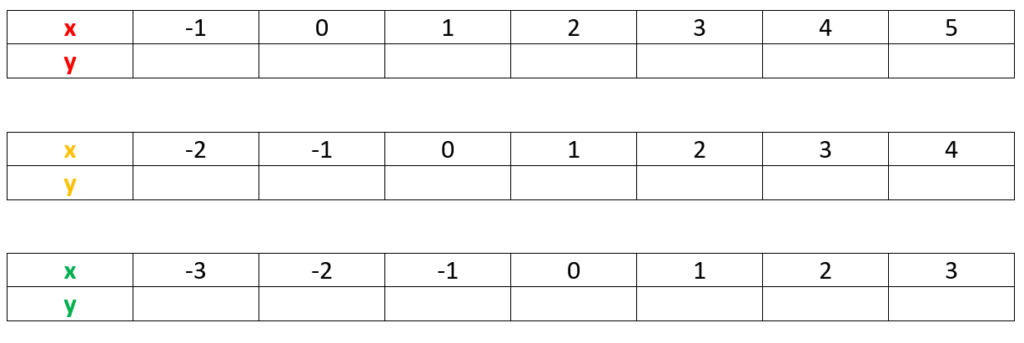
Aufgabe: Zeichne folgende Funktionsgleichungen in der angegeben Farbe!
Lösung:
Vorgehensweise:
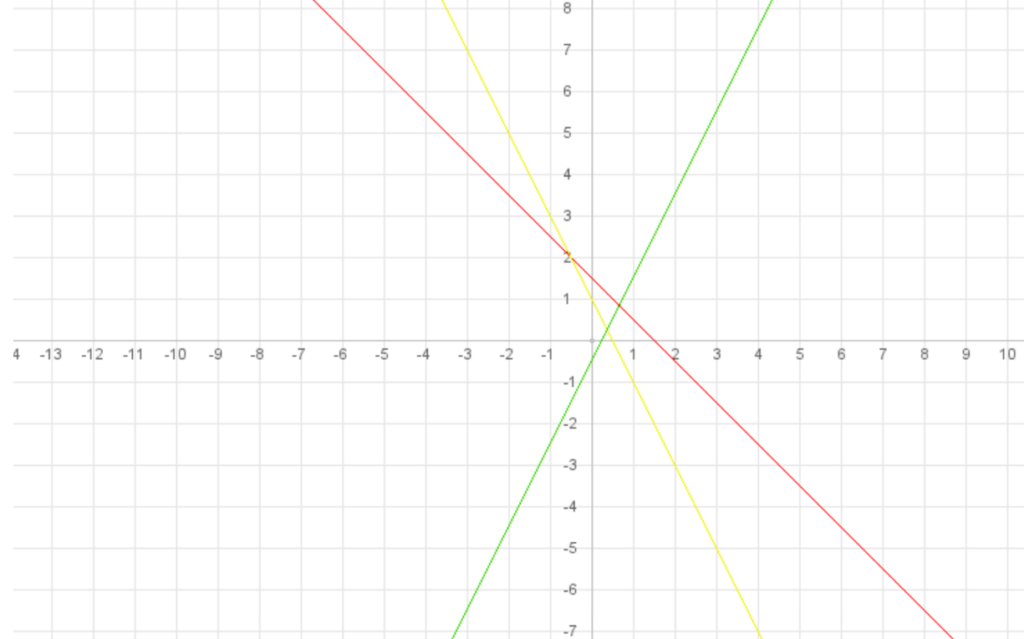
Werte vom Graphen ablesen
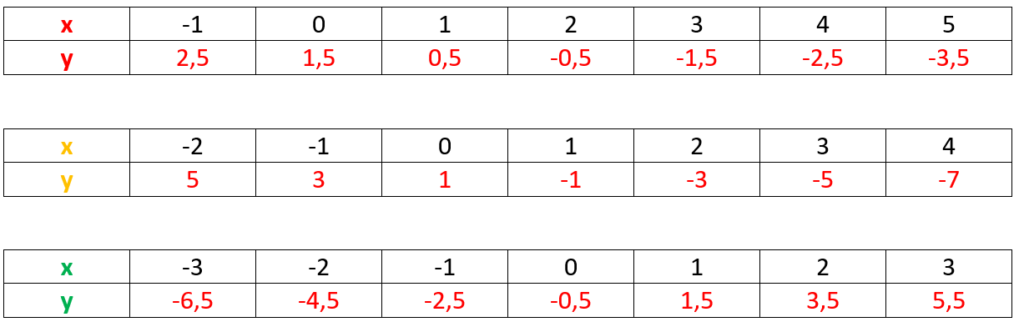
Aufgabe: Fülle die Wertetabelle mit den Werten des zugehörigen Graphen!
Lösung:
Lineare Funktionen ermitteln
Aufgabe: Gib die Funktionsgleichung an!
Ermittle die Funktionsgleichung
- mit dem Punkt P (-3 I 7) und der Steigung m = -0,25
- mit dem Punkt P (6 I 2) und der Steigung m = 8.
Lösung:
- allgemeine lineare Funktion f(x) = mx + b
in einigen Schulbüchern steht anstatt b auch n!!
- y = mx + b
Lineare Funktionen – Textaufgabe – Schwierigkeitsgrad mittel
Aufgabe:
Hansi hat morgen einen Test. Dabei wird ihn sein Lehrer mündlich zu den linearen Gleichungen abprüfen. Zur Vorbereitung bearbeitet Hansi verschiedene Aufgaben. Eine der Aufgaben lautet folgendermaßen: Die Kosten für die Erzeugung von einem Paar Ski betragen 50 Euro. Dazu kommen noch monatliche Fixkosten von 3000 Euro. Wie sieht die Funktion aus?
Lösung:
Lineare Funktionen – Textaufgabe – Schwierigkeitsgrad schwer
Aufgabe:
Anna und Sophie besuchen dieselbe Klasse. In der heutigen Mathematikstunde ging es wieder um die linearen Funktionen. So haben sie gelernt wie man nur aus Koordinaten eine Gleichung aufstellt. Als Hausaufgabe sollen sie an folgendem Beispiel das Gelernte wiederholen: Die beiden Punkte haben folgende Koordinaten: A ( 7 I 5 ) und B ( 5 I 3 ). Wie sieht die dazugehörige lineare Funktion aus?
Lösung:
📌 Möchte dein Kind lineare Funktionen sicher verstehen?
Die Lernhilfe Sprenger bietet individuelle Online-Nachhilfe mit gezielten Übungen.
Jetzt eine kostenlose Probestunde buchen und Mathe spielend meistern!