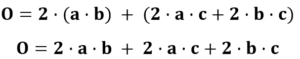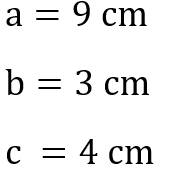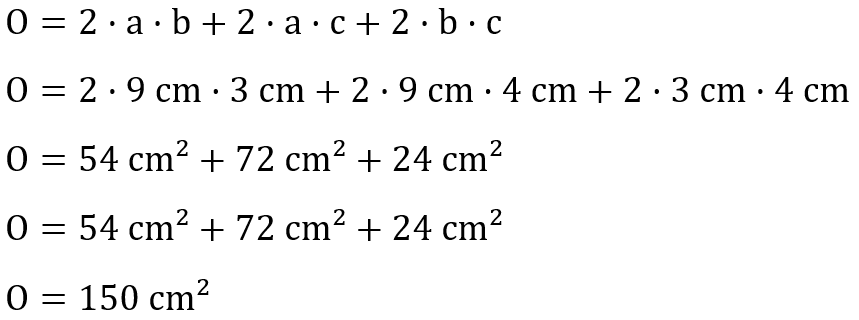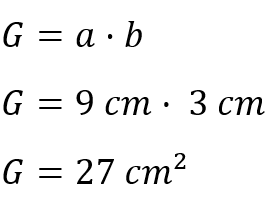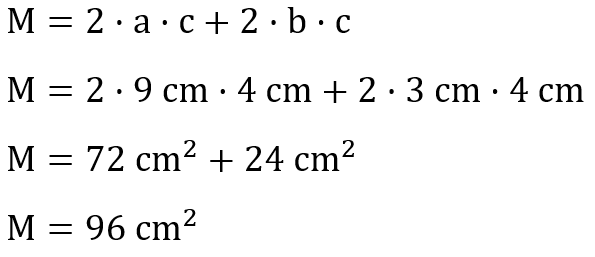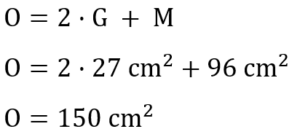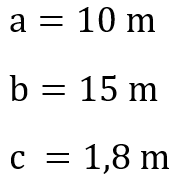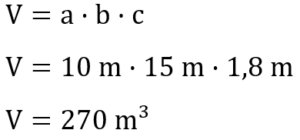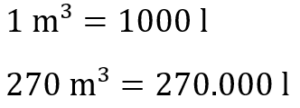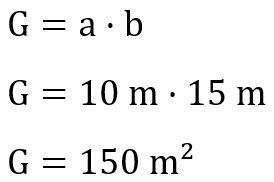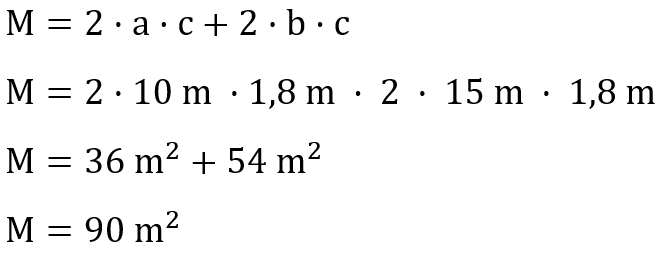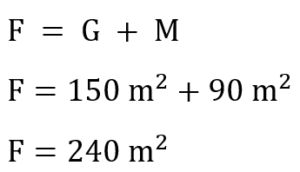Quader
Was ist ein Quader?
Ein Quader ist ein dreidimensionaler Körper mit sechs Seitenflächen. Die Seitenflächen sind alle rechteckig, wobei zwei gegenüberliegende Flächen deckungsgleich sind. Ein Quader hat zwölf Kanten, von denen jeweils vier zueinander parallel sind.
In der Regel bezeichnet man die drei maßgeblichen Kantenlängen eines Quaders mit den Buchstaben a, b und c. Arbeitet man vertieft mit Quadern, so sind auch andere Maße interessant, wie beispielsweise die Diagonale einer Seitenfläche d und die Raumdiagonale e.
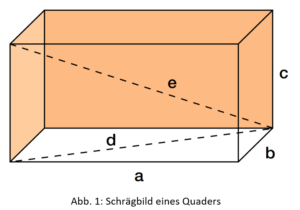
Beachte: Die Kantenlängen eines Quaders können auch mit anderen Buchstaben bezeichnet werden.
Das Volumen des Quaders
Das Volumen V eines Quaders gibt an, wie viel in einen Quader hineinpasst. Man kann es sich so vorstellen:
Würdest du einen Quader mit Wasser füllen, so gibt das Volumen an, wie viel Wasser in den Quader hineinpasst.
Berechnet wird das Volumen des Quaders mit der folgenden Formel.
In Worten sagt man auch „Länge mal Breite mal Höhe“.
Beachte: Wenn die Kantenlängen des Quaders mit anderen Buchstaben bezeichnet werden, muss man die Formel an die Buchstaben, die für die Länge, Breite und Höhe des Quaders stehen, anpassen.
Die Oberfläche des Quaders
Stellt man sich vor, dass man einen Quader in der Hand hat, so besteht die Oberfläche O aus allen Flächen, die man von außen berühren kann. Man könnte auch sagen, dass es alle Flächen sind, die man von innen berühren kann. Man muss aber darauf achten, dass bei der Oberfläche immer nur eine Seite einer Fläche gezählt wird. Die Oberfläche des Quaders berechnet man, indem man die einfache Fläche aller Seitenflächen des Quaders addiert.
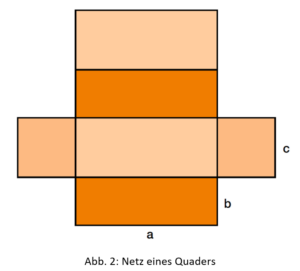
Um auf die Formel für die Oberfläche eines Quaders zu kommen, hilft es, einen Quader auseinanderzufalten, sodass wir das Netz des Quaders betrachten können.
Hier kann man erkennen, dass jeweils zwei Seitenflächen des Quaders gleich sind. Da die Oberfläche des Quaders aus Rechtecken besteht, deren Seitenlängen zu den Kantenlängen des Quaders gehören, kann man die Fläche der Rechtecke berechnen und anschließend addieren. Für die Oberfläche eines Quaders ergibt sich die folgende Formel.
Die Zahl „2“ in der Formel steht jeweils dafür, dass es zwei gleiche rechteckige Flächen von jeder Sorte gibt.
Mantelfläche und Grundfläche des Quaders
In manchen Situationen ist es notwendig, nicht die ganze Oberfläche eines Quaders zu berechnen, sondern nur einen Teil davon. Häufig unterteilt man die Oberfläche eines Quaders (und auch von Körpern im Allgemeinen) in eine Grundfläche G und eine Mantelfläche M.
Als Grundfläche bezeichnet man in der Mathematik die Fläche, auf der ein Körper steht, zumindest in der Regel. Es ist jedoch auch möglich, eine andere Seitenfläche des Quaders als Grundfläche zu wählen. In unserem Quader ergibt sich für die Grundfläche Folgendes:
Beachte: Ein Quader kann auf unterschiedliche Seitenflächen gestellt werden, womit als Grundfläche auch eine der anderen Seitenflächen des Quaders gewählt werden kann.
Als Mantelfläche bezeichnet man die Summe aller Seitenflächen eines Quaders. Für die Mantelfläche unseres Quaders ergibt sich folgende Formel.
Versuche mithilfe der Abbildungen 1 & 2 nachzuvollziehen, welche der Flächen in unserem Quader nun zur Mantelfläche gehört.
Beachte: Wie auch bei der Grundfläche hängt die Mantelfläche davon ab, welche Flächen man tatsächlich als Mantelfläche wählt. Was man sich merken sollte ist, dass Grundfläche und Mantelfläche nie übereinander liegen.
Wir können die Oberfläche auch berechnen, indem wir die Grundfläche und die Mantelfläche zusammenrechnen. Dabei müssen wir beachten, dass eigentlich noch der „Deckel“ unseres Quaders, welcher der Grundfläche gegenüber liegt, fehlen würde. Aber weil wir wissen, dass gegenüberliegende Flächen gleich sind, können wir die Grundfläche zweimal zählen. Gemeinsam mit der Mantelfläche ergibt sich so die Oberfläche des Quaders.
Wenn man nun die Formeln für Grundfläche und Mantelfläche einsetzt, kommt man wieder auf die uns bekannte Formel für die Oberfläche.
Nun sind wir bestens vorbereitet, um einige Beispielaufgaben zu rechnen.
📌 Hat dein Kind Schwierigkeiten mit diesen Formeln?
Die Lernhilfe Sprenger bietet Online-Nachhilfe an, um mathematische Themen anschaulich und verständlich zu vermitteln – in kleinen Gruppen oder als Einzelnachhilfe!
Beispielaufgaben zum Quader
Beispielaufgabe 1: Eine Basisaufgabe zum Quader
„Ein Quader ist 9 cm lang, 3 cm breit und 4 cm hoch. Berechne das Volumen und die Oberfläche des Quaders.“
Lösung:
Wir notieren uns zunächst die benötigten Informationen aus der Aufgabe. Uns ist bekannt, dass wir für die Oberfläche und das Volumen die drei Kantenmaße benötigen.
Das Volumen
Für das Volumen gilt die im ersten Abschnitt angegebene Formel. Nun müssen wir nur die passenden Werte in diese Formel einsetzen.
Damit hat unser Quader ein Volumen von 108 cm³.
Beachte: Wenn wir Einheiten in unseren Rechnungen haben, so werden sie genauso wie Zahlen zusammengerechnet und anschließend wieder an das Ergebnis geschrieben. Beispiel: 1 cm · 1 cm = 1 cm² ; 1 cm + 1 cm = 2 cm oder 2 m · 3 m · 4 m = 24 m³.
Die Oberfläche
Auch für die Oberfläche können wir nun die passenden Werte in die uns bekannte Formel einsetzen.
Der Quader hat also eine Oberfläche von 150 cm².
In manchen Aufgaben ist zunächst nach der Grundfläche und der Mantelfläche eines Quaders gefragt. Wir berechnen nun separat die Grundfläche G und die Mantelfläche M dieses Quaders. Wir fangen mit der Grundfläche an.
Der Quader hat also eine Grundfläche von 27 cm².
Nun benötigen wir noch die Mantelfläche. Wieder setzen wir die Werte in die richtige Formel ein.
Mithilfe dieser Werte kann nun die Oberfläche bestimmt werden, so wie es oben bereits erklärt wurde.
Hier kann man sich verdeutlichen, dass bei beiden Wegen der gleiche Wert für die Oberfläche herauskommen muss.
Für diesen Quader war die Rechnung noch recht simpel. Im Folgenden betrachten wir eine etwas komplexere Aufgabe, die an den Alltag angelehnt ist.
Beispielaufgabe 2: Eine Textaufgabe zum Quader
„Zu Beginn der Freibad-Saison soll das Hauptschwimmbecken erneuert und anschließend mit Wasser befüllt werden. Dieses Schwimmbecken ist 10 m breit und 15 m lang. Die Wassertiefe beträgt 1,8 m, wobei das Becken bis zum Rand gefüllt ist.
- a) Wie viel Wasser passt in das Schwimmbecken?
- b) Das Schwimmbecken soll komplett neu gefliest werden. Dazu werden 25 x 25 cm Fliesen verwendet. Wie viele solcher Fliesen werden benötigt?“
Lösung:
Das Schwimmbecken in diesem Beispiel hat die Form eines Quaders. In der Teilaufgabe a) ist gefragt, wie viel Wasser dort hineinpasst. Das bedeutet, es ist nach dem Volumen gefragt, welches wir nun berechnen. Auch hier notieren wir uns zunächst die für uns wichtigen Maße.
Beachte: Die Buchstaben können bei dieser Aufgabe frei gewählt werden. Wir könnten also auch sagen a = 15 m, b = 1,8 m und c = 10 m. Wir müssten bei Teilaufgabe b) nur darauf achten, was wir als Grundfläche und was wir als Mantelfläche wählen und die Formel ggf. anpassen.
Wir setzen unsere Werte in die Formel ein.
Da nach Litern (l) gefragt ist, müssen wir das Volumen in m³ in l umrechnen.
In das Schwimmbecken passen insgesamt also 270.000 l.
In der Teilaufgabe b) ist nach der Anzahl der Fliesen gefragt, die zur Erneuerung des Schwimmbeckens verwendet werden soll. Hierzu müssen wir zunächst in Erfahrung bringen, wie groß die geflieste Fläche ist. Dass es nicht einfach nur die Oberfläche unseres Quaders ist, werden wir gleich sehen.
Zunächst berechnen wir unsere Grundfläche, welche den Boden des Schwimmbeckens darstellt.
Beachte: Hätten wir hier als Maße a = 15 m, b = 1,8 m und c = 10 m gewählt, so würde sich für die Grundfläche gelten G = a · c und für die Mantelfläche M = 2 · a · b + 2 · c · b.
Als Nächstes müssen wir wissen, wie groß die Seitenflächen des Schwimmbeckens sind. Diese Seitenflächen sind die Mantelfläche des Quaders.
Beachte: Hätten wir vorher als Maße a = 15 m, b = 1,8 m und c = 10 m gewählt, so würde für die Grundfläche gelten G = a · c und für die Mantelfläche M = 2 · a · b + 2 · c · b.
Nun müssen wir die Grundfläche und die Mantelfläche zusammenrechnen, um auf die zu fliesende Gesamtfläche zu kommen. Man beachte hierbei, dass das Schwimmbecken sozusagen keinen „Deckel“ hat. Das heißt für die Fläche F, die gefliest werden soll, ergibt sich Folgendes.
Beachte: Hier wurde der Buchstabe „F“ für die Fläche gewählt, um deutlich zu machen, dass sich die Oberfläche in diesem Beispiel von der Oberfläche eines mathematischen Quaders unterscheidet, weil uns hier der „Deckel“ fehlt.
Im letzten Schritt muss nun bestimmt werden, wie viele Fliesen benötigt werden.
Für die Erneuerung des Schwimmbeckens werden also insgesamt 3840 Fliesen benötigt.
Quader im Alltag
Quader tauchen im Alltag in den verschiedensten Zusammenhängen auf, weswegen es in vielen Berufen oder auch im privaten Bereich (z. B. beim Streichen eines Zimmers) notwendig ist, Volumen und Oberfläche berechnen zu können. Typische Quader sind Zimmer, Schränke, Aquarien, Schachteln, Schubladen oder auch Backsteine.
📌 Möchtest du, dass dein Kind den Quader sicher versteht?
Die Lernhilfe Sprenger bietet individuelle Online-Nachhilfe mit gezielten Übungen.
Sichere dir eine kostenlose Probestunde und erleichtere deinem Kind das Lernen!